【平均律・純正律】G#とAbは何が違う？
厳密に言うと、実は違う音ってホント？
今回はこのような疑問にお答えする内容です。
AbとG#は、文字は違えど、ピアノの鍵盤で言うと同じ音です。
しかし、厳密に言うとこの２つの音は「違う音」です。
一体何が違うのでしょうか？
今回は、数字を厳密に計算していきながら解説していきます！
（計算式が出てきますが、数字に苦手意識のある方もとりあえず一通りざっくり見てみると、G#とAbが違う理由がざっくりわかってきます）
スポンサードサーチ
「平均律」とは？
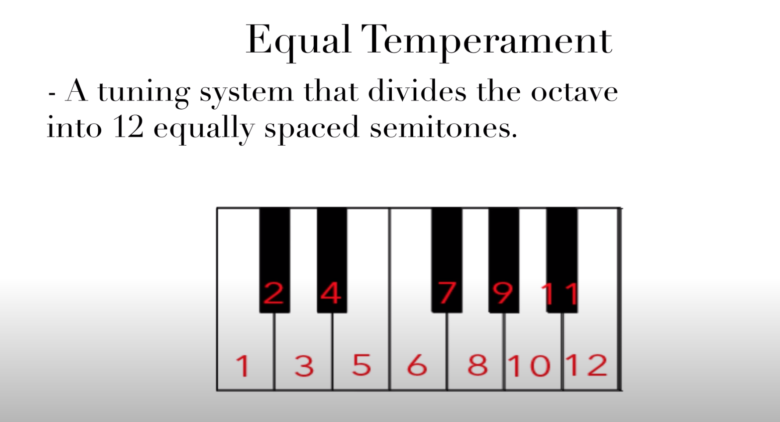
画像：動画より
平均律とは、1オクターブを均等に12個に分ける音律のことを指します。
平均律では、半音１つ=100セントという単位で区切られています。
この半音=100セントという数字を使えば、「五度圏で右に一個ズレる度に完全５度の差が出て、完全5度ずつ右に回ると最終的にピッタリ一周回れる」という法則も成立します。
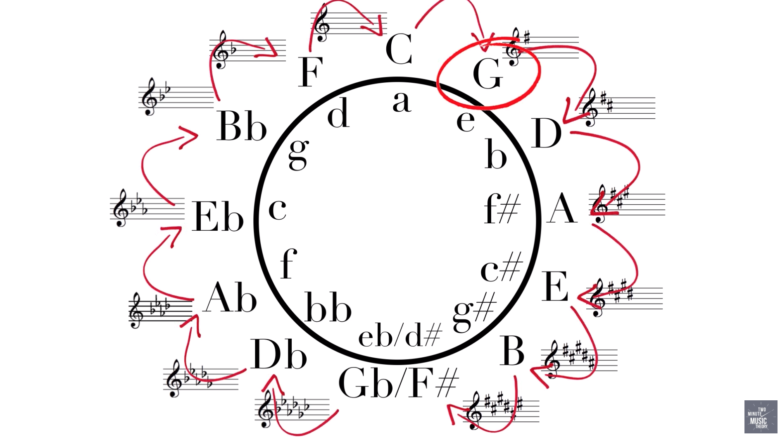
画像：動画より
五度圏についてはこちらで詳しく解説しています↓
ピタゴラス音律とは？
数学的にいうと、1オクターブ=2/1（つまり2倍）、完全5度は2/3という数式で表せます。
これは「ピタゴラス音律」と呼ばれ、周波数を2/3（3:2）、つまり完全5度で連続させて作る音律です。
平均律は1オクターブを12で割っていますが、ピタゴラス音律では周波数に2/3をかけて計算します。
センターをD（294.0）と考えると…
ピタゴラス音律では、周波数294.0=Dを中心と考えます。
中心ですので、比率は1:1と考えます。
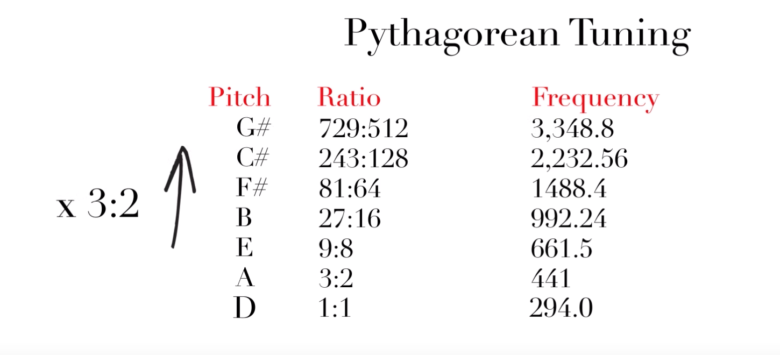
画像：動画より
このDを起点に、2/3ずつ数字をかけていくと、綺麗に完全5度ずつ、五度圏と同じようにD→A→E→B…という順番になります。
音を下げる時は、2/3ずつ数字を割って算出します。
画像：動画より
オクターブはぴったり2倍
オクターブの場合は、2:1、つまり2倍もしくは２分の１の数字になります。
例えばAのオクターブは、441を起点にすると１オクターブ上は882、１オクターブ下は220.5となります。
画像：動画より
スポンサードサーチ
比率がどんどん複雑になっていく
さて、表を見るとわかりますが、より音が高くなっていく・低くなっていくにつれて、Ratio（比率）の数字がどんどん複雑になっています。
言い換えると、複雑になっていくにつれて音が少しずつ「ズレている」ように感じます。
たとえば、このピタゴラス音律でDの長3度上にあたるF#の音の比率は81:64で、「3:2」のようにわかりやすい数字ではなくなっています。
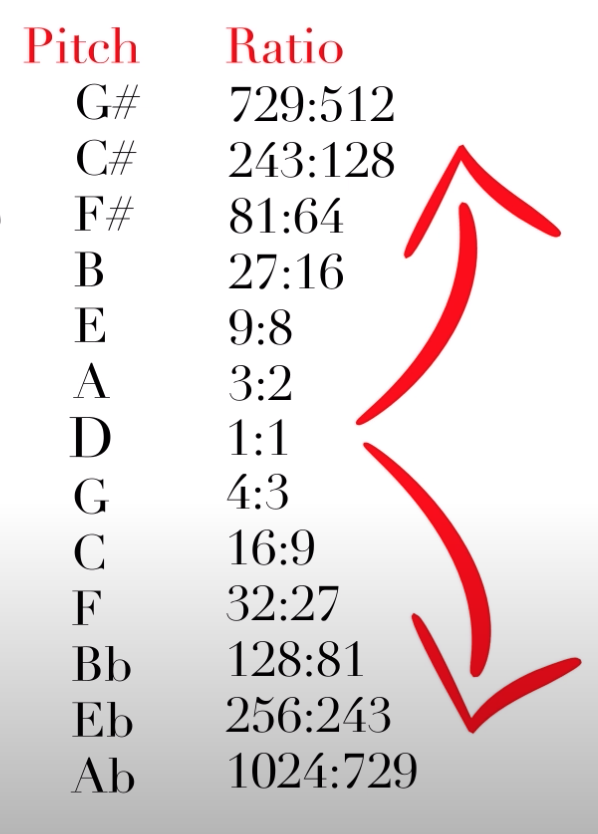
画像：動画より
2音ではなく3音の和音だとキレイに聞こえる
ルート+長3度の音を2音だけ鳴らすと、かなり違和感の音があるようになります。
しかし5thの音を足して「メジャーコード」のようにコードで鳴らすと、スッキリした響きになります。
実際の音を聞いてみましょう↓（1:56~2:00）
別の問題「長2度のとき」
実は、この音律にはこの他にも別の問題があります。
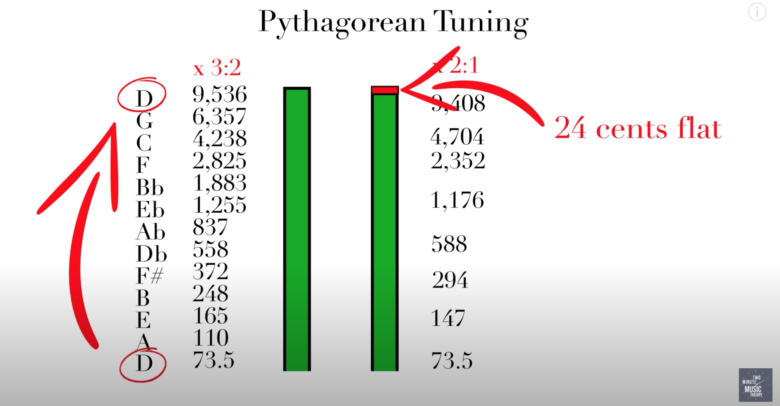
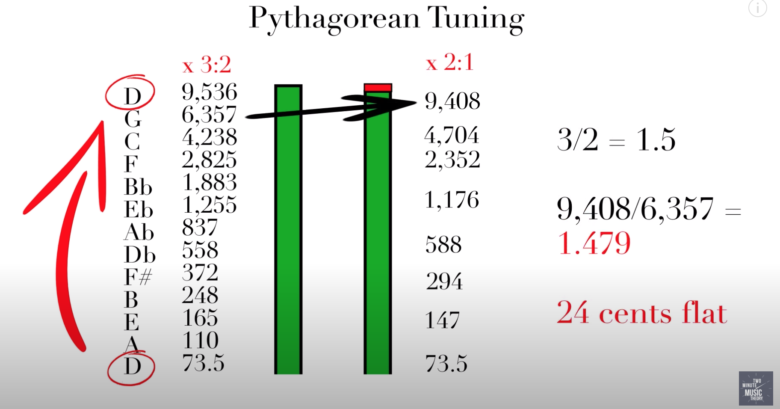
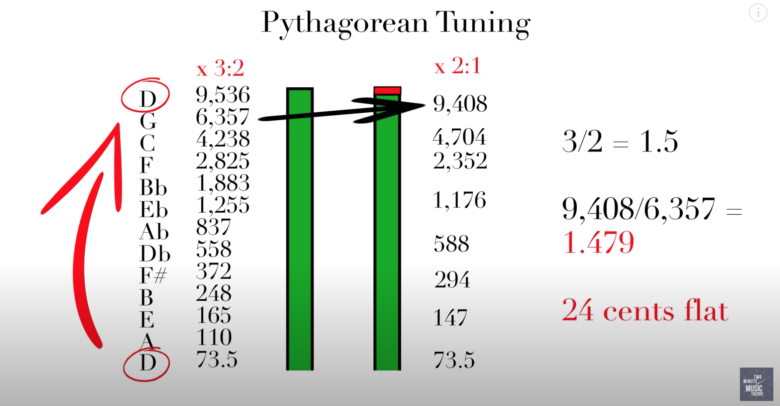
たとえばDの音（周波数は72.5）を起点とし、ひたすら2/3をかけていきましょう。
こうすると、1オクターブ上のDの周波数は「9,536」になります。
1オクターブ上なら、ピアノの鍵盤を弾いた時のように、ぴったり合っているような響きになりそうです。
しかし、実は2/3ずつかけていくと、本来完璧な音になるはずの音程より24セント音程が低くなってしまうのです。
半音1個＝100セントですから、音程が1/4もズレてしまうことになります。
画像：動画より
ピタゴラスコンマ
このように、ピタゴラス音律において完璧な音程と差が出てしまうこの音律独特の音を「ピタゴラスコンマ」といいます。
コンマ（Comma）は「音程」という意味
画像：動画より
ちなみに、１オクターブ上のDの一つ手前であるGの時点で、すでにズレが生じます。
Dと一緒に鳴らすと、このズレによって違和感のあるうなりが出てくるため、狼の鳴き声にちなんで「ウォルフ・フィフス（Wolf Fifth）と呼びます。
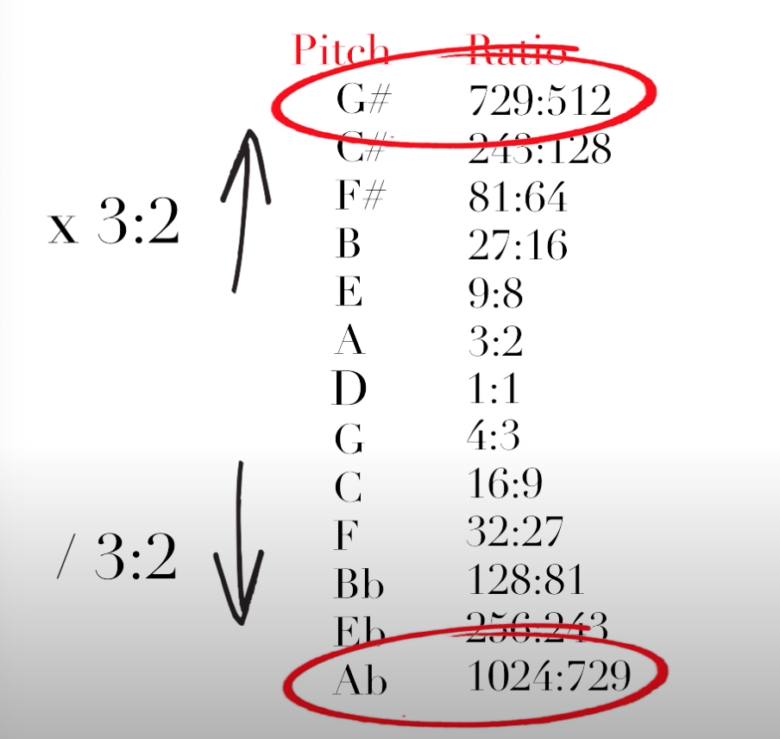
G#とAbを見てみよう
さて、ここでピタゴラス音律におけるAbとG#を見てみましょう。
画像：動画より
先ほどのDの例のように、ピタゴラス音律の計算の仕方だと、ちょうど１オクターブの差でもズレが生じ、音にうねりが出てしまいます。
ちなみにAbはAugumented 5th、G#はDiminished 5thと捉えられますが、これはDに対するトライトーン（増４度）の音にあたります。
ピタゴラス音律が正確でないのなら、新しい基準を作ろう
さて、ここまでの解説で、ピタゴラス音律ではズレが生じ、美しい和音を作ることができないということがおわかりいただけたかと思います。
ではどうしたらいいのか？
このピタゴラス音律の問題を解決するのが、「純正律」です。
スポンサードサーチ
純正律とは？
純正律はハーモニーを美しく奏でるために調整された音律です。
先ほどの長３度の音程にあたる２つの音を同時に鳴らしても、うねりがなく綺麗に鳴るようになります。
また、先ほどの比率の計算においても、ピタゴラス音律よりも簡潔に、綺麗にまとまった数値になります。
純正律ではどうやって数字を調整してるの？
ピタゴラス音律の数字を綺麗に調整した純正律は、先ほど出てきた「ピタゴラスコンマ」をかけることにより、俗に言う「キレイな」数字になります。
81/64という複雑な数字が、81/80（ピタゴラスコンマ）で割ることにより、5/4という非常にスッキリした数字になるのです。
（動画では「(81/64) x (81/80)」となっていますが、コメント欄で間違いの指摘があり、正しくは「(81/64) ÷ (81/80)」となります。）
音も、このように綺麗に聞こえるようになります↓（3:20~）
数字を調整することで、たとえばAをベースにした倍音を考えた時も、長3度の関係にある4番目と5番目の音であるAとC#が綺麗に鳴るようになります。
画像：動画より
純正律では、すべての長3度の和音を美しくひびかせるために、5/4をかけて数を調整します。
たとえばCを起点とした場合、5/4をかけてE、Eに5/4をかけてG#…のようにしていきます。
純正律の問題点
しかし、ここで一つ問題が生じます。
Cの周波数は261で、5/4をかけると326.25になります。
しかし、もし純音のEを計算するため、完全5度を計算するときに使った「3/2」をかけた場合と比べると、純正律におけるEが周波数でいう4（22セント）ほどズレていることがわかります。
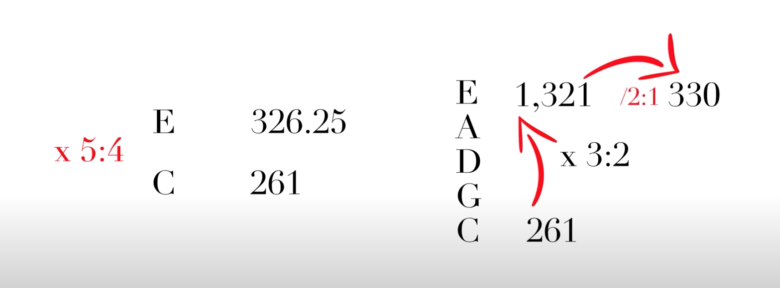
画像：動画より
1オクターブ上のE：1321
1オクターブ下のEで、上記のCと一番近いE：2で割ると330
このように、音の組み合わせによっては発生する、純正調3度と計算した長3度ズレのことを「シントニックコンマ」と呼びます。
ピタゴラス音律と純正律で発生するズレ
つまり、ピタゴラス音律と純正律においては、このようなズレが発生します。
純正音に対して22セントのズレ：シントニックコンマ（純正律）
そして、このピタゴラスコンマとシントニックコンマの差「2セント」のことを「スキスマ」といいます。
純正律におけるG#とAb
さて、ここでG#とAbについて見てみましょう。
Cの長3度上に当たる音はE、Eの長3度上にあたる音はG#です。
一番下のCと一番上のG#の音の関係は「増5度」です。
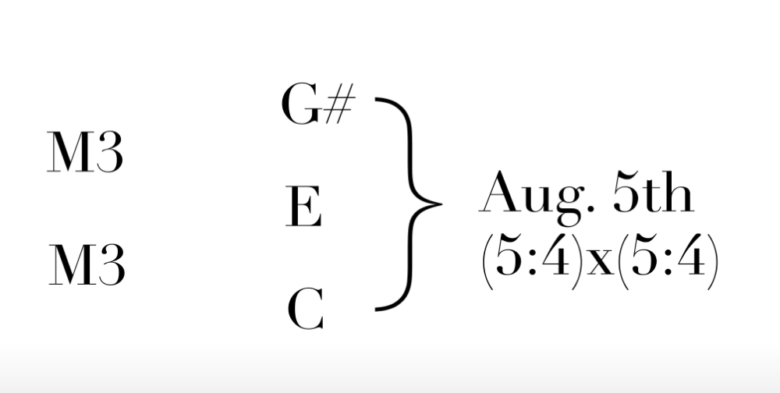
画像：動画より
しかし、CとAbの場合は短6度の関係にあることがわかります。
倍音表を見ると、5番目と8番目の音で、比率は8:5になります。
純正律の場合、長3度上に上がるに従って5/4を周波数にかけて計算していきます。
CからE、EからG#と計算すると、最終的には25:16（25/16）をかけていることになり、G#の周波数は407.81になります。
実際の音↓（5:03~5:13）
しかし、短6度の場合はCと8:5の距離にありますから、C（261）に8/5をかけた数値が「Ab」となります。
すると、Abは「417.6」になります。
G#を計算した時は「407.81」でしたので、10ほどの差が出てしまいました。
そう、「増5度を計算するときの式」と「短6度を計算するときの式」は違うので、同じ音程なのに結果が変わってしまうのです。
どれぐらい違うか、実際の音を聞いてみましょう↓（5:13~5:16）
実は、昔の楽器は鍵盤を1オクターブ19個（今は12個）揃え、この問題に対応できるようにしていたのです。
ちなみにこちらのサイトでは、19 TET鍵盤の音を実際に体験することができます↓
https://academo.org/demos/19-tet-keyboard/
しかしいずれにせよ、純正律ではハーモニーを美しく演奏するために、キーをかんたんに変えることができません。
たとえばCメジャーキーに合わせて完璧に調整したとしても、Abメジャーキーでそのまま演奏したら音がズレてしまうのです。
G#=Abになった理由
前述の通り、Abの音は増5度の時よりも音が大きくズレてしまうため、ゆくゆくは音階から外れ、現在は「G#=Ab」として扱われるようになりました。
一時期は純正律に対応した楽器も出ていましたが、最終的には現在のように平均律で調律するところに落ち着きました。
そして、1オクターブ=12鍵盤の楽器が主流となっていきます。
スポンサードサーチ
平均律=完璧ではない
ここまでを考えると、平均律は単に半音=100セント、1オクターブ12音で均等に区切っただけですから、正確にいうと「純音」ではないことがわかります。
たとえば、平均律だと各音がそれぞれこれぐらい微妙にズレてしまいます。
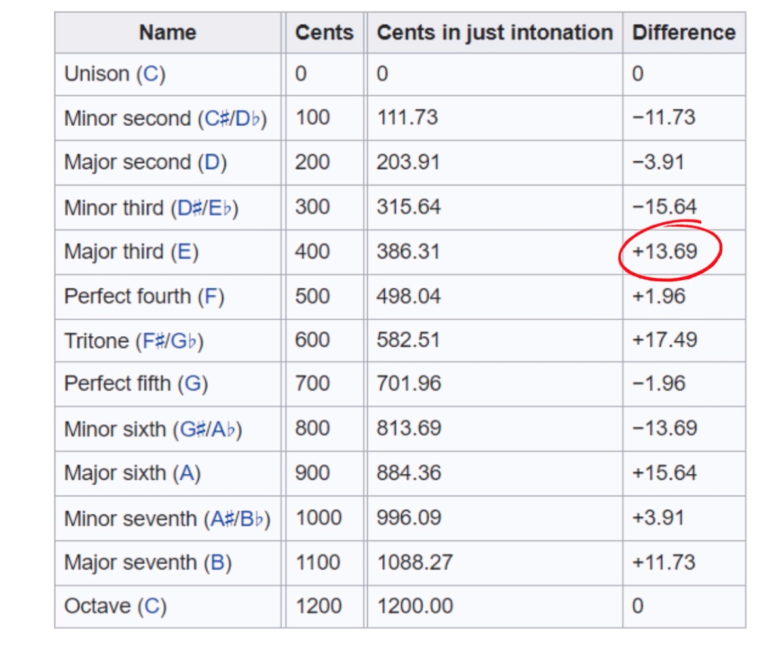
画像：動画より
しかし、そこまで大きな差にはならないので、許容範囲です。
加えて、純正律だと複雑な計算をしなければならず、鍵盤数も増やさなければいけませんので、手軽さで言ったら平均律の方がよいですし、産業的にも鍵盤楽器が作りやすいです。
このような理由で、現在の鍵盤楽器は平均律で作られており、Ab=G#という認識になっているのです。
ちなみにこちらの動画では、平均律で和音を弾くとどれぐらい「うねり」が出るかを可視化していて面白いです（Justonicは純正律、Temperedは平均律という意味です）↓
平均律を嫌う人も
しかし、やはりハーモニーが綺麗に聞こえなくなる平均律を嫌がる人もいます。
実際に現代音楽の作曲家であるHarry Partchは「平均律は、カオスを生み出す基本原理だ」と言及しています。
平均律と純正律が共存する今
しかし、平均律のおかげで最近の西洋音楽が発展してきたのは間違いありません。
また、鍵盤楽器は平均律が基本となりましたが、純正律は今でもオーケストラでも使われています。
ただし、オーケストラにピアノがある場合は、ピアノは平均律で調律されていますので、オーケストラ側が平均律に合わせた演奏をしなければいけません。
このように難しい部分もありますが、今回の記事を通して、どちらもよいところがあること、G#とAbの厳密な違いがお分かりいただけたかと思います。
特にオーケストラに関わりが出てきたときは、ぜひ今回の記事の内容を思い出してみてください！
音楽と科学・数学についてもっと学んでみたいという方には、こちらがおすすめです↓
-
前の記事
【音楽理論】モノフォニー・ポリフォニー・ホモフォニー・ヘテロフォニー・テクスチュアとは？ 2020.10.03
-
次の記事
【かっこいいコード進行】エモいコードを作る方法５連発！【作曲】 2020.10.05
